[AI 학습노트] 누구나 이해할 수 있는 머신 러닝 모델

원문 보기: An explanation of machine learning models even you could understand

이 글은 다섯 살의 어린아이도 이해할 수 있는 글을 쓰고자 하는 저의 두 번째 글입니다.

쓰다 보니, 다섯 살을 이해시키는 것은 꽤 힘들다는 것을 알았습니다. 그래서 이 글이 유치원생이 이해하기는 어렵더라도, 데이터 과학에 대한 지식이 없는 사람들에게는 도움이 되었으면 좋겠습니다.

먼저 기계학습의 여러 종류로 기계학습이 무엇인지 설명한 다음, 모델로 넘어가겠습니다. 수학적인 개념은 다른 글에서 따로 다룰 생각입니다. 재밌게 읽어주세요!

기계학습의 정의

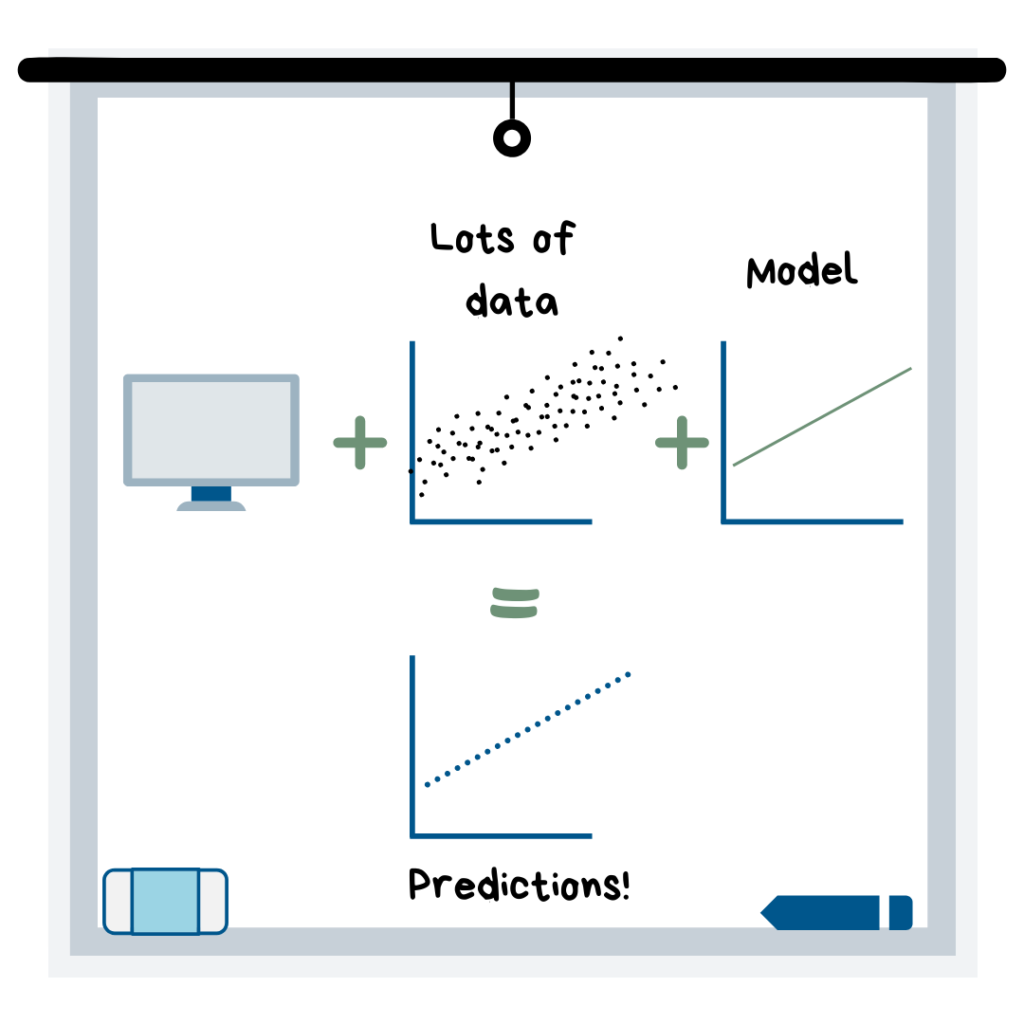
기계학습의 정의

우리가 많은 양의 데이터를 컴퓨터 프로그램에 로드하고, 데이터에 적합한 모델을 고를 때 기계학습은 인간의 도움 없이 스스로 예측하여 적합한 모델을 찾아냅니다. 컴퓨터는 알고리즘을 통해 모델을 만들어내는데, 이때 알고리즘에는 단순한 방정식부터 매우 복잡한 논리/산술 작업을 수행할 수 있는 다양한 알고리즘이 존재합니다.

참고 : 인공지능과 기계학습의 차이

기계 학습은 인간이 사용할 모델을 선정하고 약간 손을 봐주면 그 모델을 사용하여 데이터에서 패턴을 학습합니다. 그런 다음 새로운 데이터를 입력하면 결과를 예측해 줄 것입니다!

지도학습(Supervised machine learning)의 정의

지도학습은 모델에 넣어준 데이터를 ‘라벨링’하는 기계학습의 일종입니다. 라벨링 되었다는 것은 단순히 결과를 알고 있다는 뜻입니다. 예를 들어, 만약 모델이 당신의 친구가 골프를 칠지 아닐지를 예측하기 위해 온도, 요일과 같은 변수들이 필요할 것입니다. 만일 데이터가 라벨링이 되어있는 경우 당신의 친구가 실제로 골프를 쳤다면 각 변수가 1의 값을 가질 것이고, 골프를 치지 않았다면 0의 값을 가지게 될 것입니다.

비지도학습(Unsupervised machine learning)의 정의

예상한대로, 비지도 학습은 지도학습에 반대되는 개념입니다. 지도학습을 통해서 우리는 당신의 친구가 골프를 치러 갔는지 안 갔는지 알 수가 없습니다. 모델을 통해 어떤 일이 일어났는지 추측하거나, 일어날 지 예측하는 것은 오로지 컴퓨터에 달려있습니다.

지도학습 모델
회귀 분석(Logistic Regression)

회귀 분석은 예 / 아니오 혹은 1~10점 사이의 고객 만족도와 같은 범주로 구성된 대상을 분류할 때 사용됩니다.

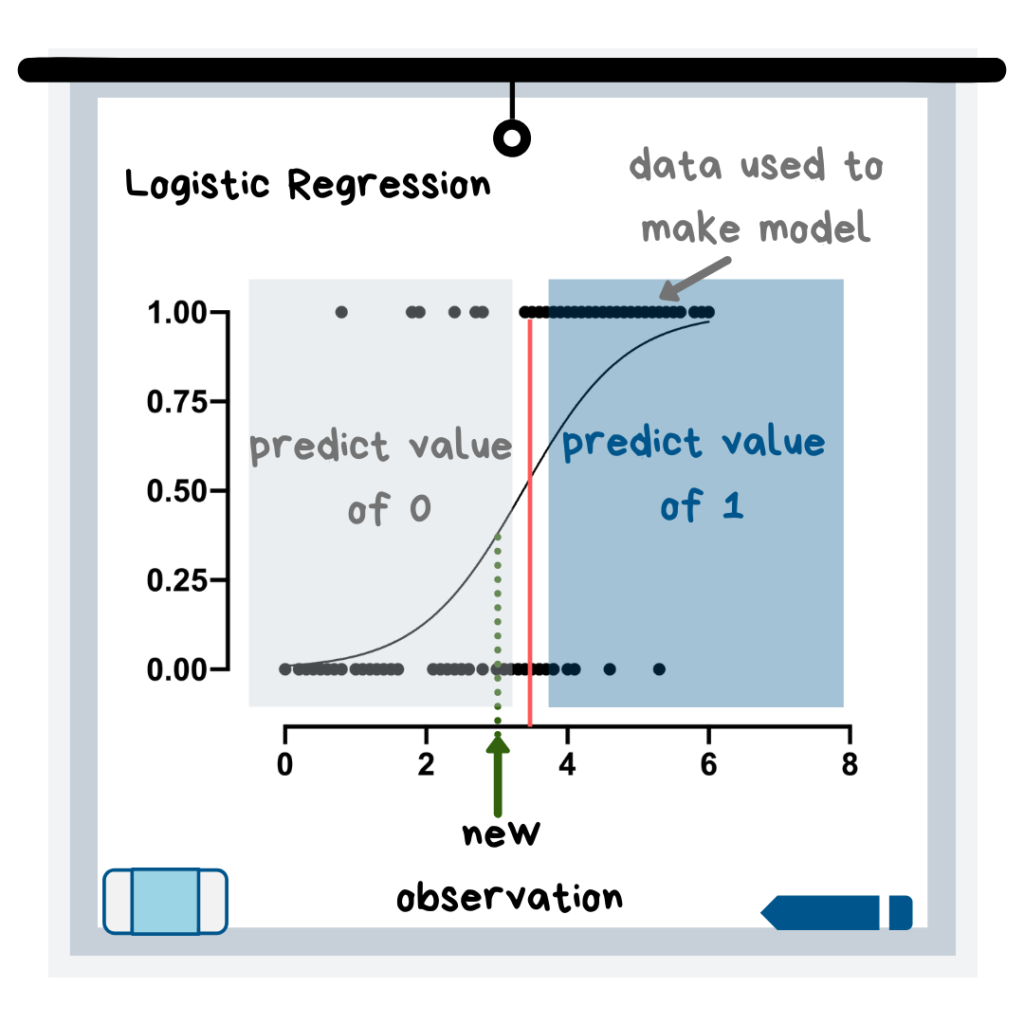
회귀분석 개념도

위의 그래프에서 ‘new observation’은 곡선의 왼쪽에 있으므로 0의 예상 값을 가질 것입니다. 곡선의 기반이 되는 데이터를 보면 이해가 쉬울 것입니다. 그림의 ‘predict value of 0’의 영역 대부분의 데이터가 0의 y값을 가지기 때문입니다.

선형 회귀(Linear Regression)

선형 회귀는 머신 러닝을 처음 배우는 사람들이 쉽게 접하는 기계 학습 모델 중 하나입니다. 선형 회귀에 사용되는 알고리즘은 비교적 이해하기 쉽기 때문입니다. 단순히 초등학교에서 배우는 개념인 적정선을 사용하여 결과를 예측할 수 있습니다. (아래 그림 참고)

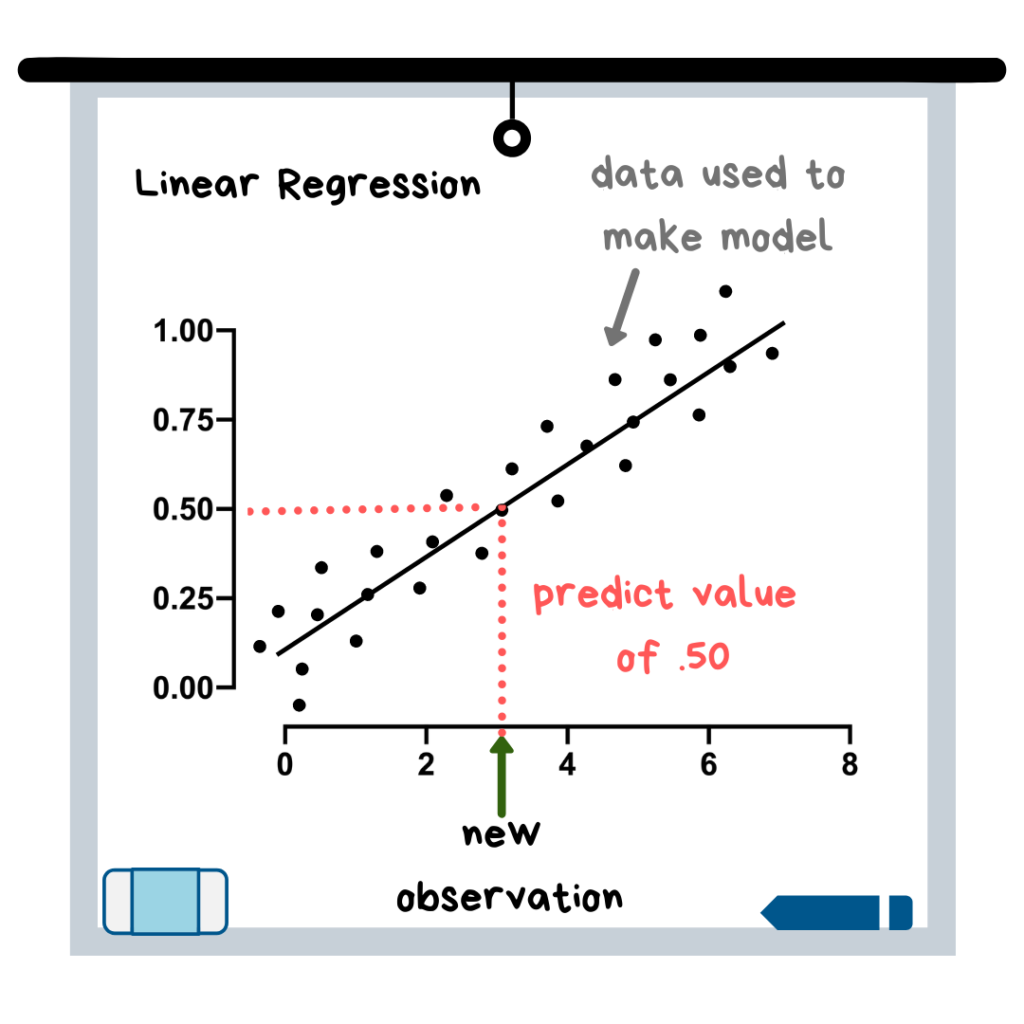
선형회귀분석 개념도

선형 회귀는 로지스틱 회귀 분석과 유사하지만, 목표 변수가 연속적일 때 사용되므로 y는 모든 값이 될 수 있습니다. 실제로 연속적인 목표 변수를 가진 모델은 전부 ‘회귀’로 분류될 수 있습니다. 주택의 가격이 연속적 변수의 사례가 될 수 있습니다.

선형 회귀 또한 수식을 통해 해석할 수 있습니다. 모델의 회귀 방정식에는 각 변수에 대한 계수가 포함되며 이 계수는 독립 변수(x)의 작은 변화에 대해 대상 변수가 얼마나 많이 변하는지 나타냅니다. 주택 가격의 회귀 방정식을 보고 다음과 같이 말할 수 있을 것입니다. “집 크기(x)가 1피트 증가 할 때마다 판매 가격(목표 변수)은 25달러 증가한다.”

K 최근접 이웃(K Nearest Neighbors, KNN)

이 모델은 분류 혹은 회귀 두 가지에 모두 사용될 수 있습니다. 이 모델은 우선 모든 데이터를 그래프에 표시합니다. 모델 이름의 ‘K’는 예측 결과를 결정하기 위해 모델에서 가장 가까운 데이터 포인트 개수를 나타냅니다. (아래 그림 참조). K값을 선택함으로서 어떤 것이 가장 정확한 예측을 하는지 알 수 있습니다.

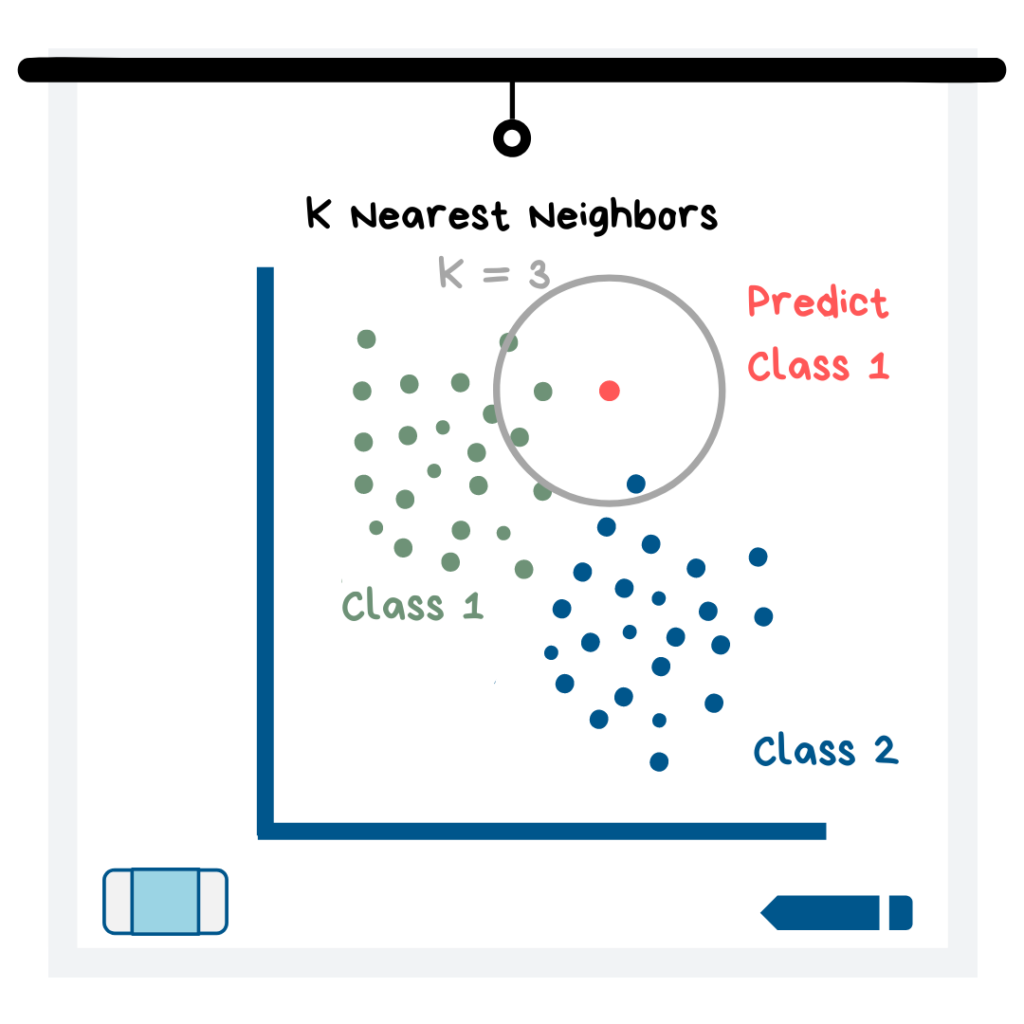
K 근접이웃 개념도

‘K = N’ 원 안에 있는 모든 데이터는 새로운 데이터 포인트에 대한 목표 변수 값이 무엇이어야 하는지에 대한 ‘투표’가 됩니다. 가장 많은 투표를 받은 값이 K-근접이웃이 새로운 데이터 포인트에 대해 예측한 값입니다. 위의 그림을 보면 원 내부의 2개의 데이터는 class 1에 속해있고, 1개의 데이터는 class 2에 속해있습니다. 따라서 이 모델은 새로운 데이터 포인트가 class 1에 속한다고 예측할 것입니다. 만약 모델이 범주 대신 숫자 값을 예측하려고 하는 경우 원 내부의 데이터는 평균을 내기 위한 숫자 값이 될 것입니다.

서포트 벡터 머신 (SVMs)

서포트 벡터 머신은 데이터 포인트 사이의 경계를 만들어 작동하는데, 한 클래스의 대부분이 경계의 한 쪽에 속하고 다른 클래스의 대부분이 다른 쪽에 속하도록 경계를 설정합니다.

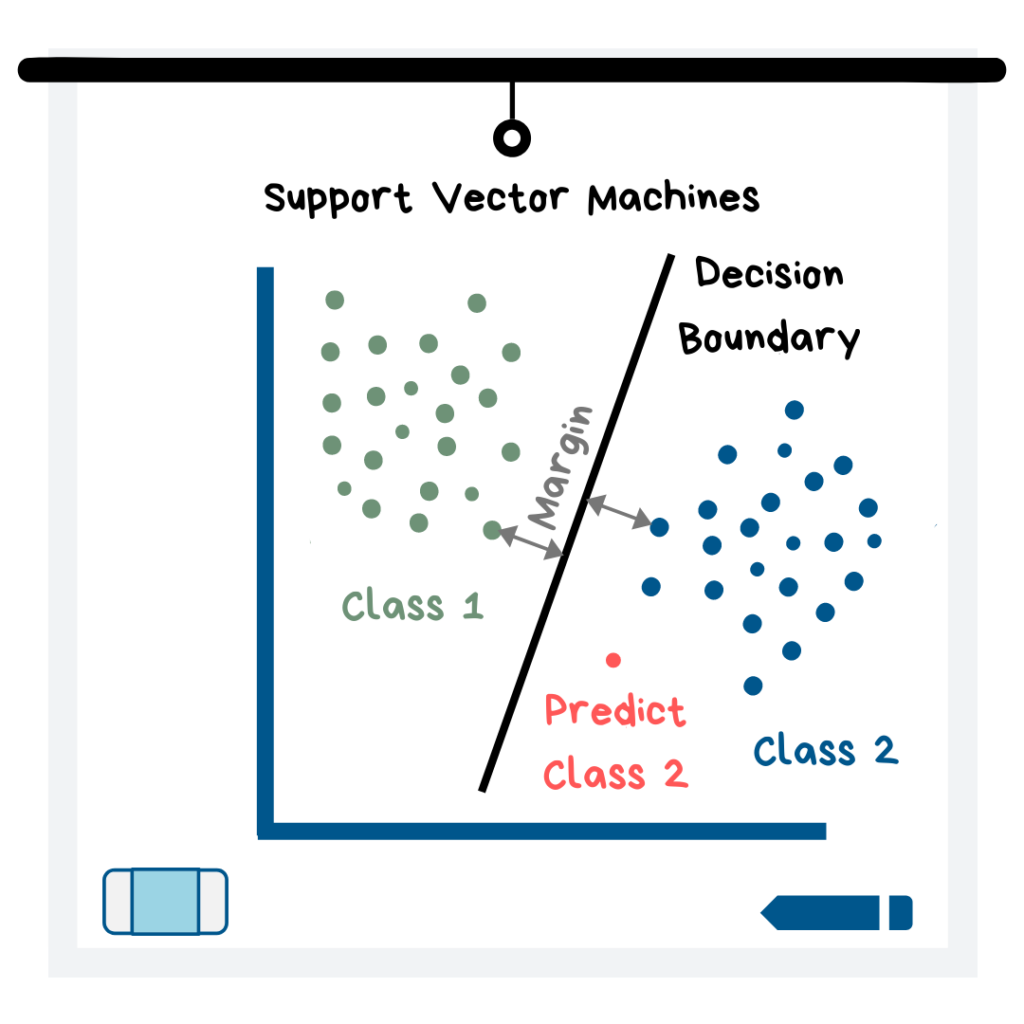
서포트 벡터 머신(SVMs) 개념도

이 모델이 작동하는 방법은 모델이 가장 큰 마진을 가진 경계를 찾는 것입니다. 이때 마진은 경계와 가장 가까운 포인트와 경계 사이의 거리를 뜻한다. 위 그림 참조). 그래프에 표시된 데이터는 경계의 어느 쪽에 있는지에 따라 클래스가 결정될 것입니다.

모델이 분류에 사용될 경우만을 설명했는데, 서포트 벡터 머신은 회귀에도 사용이 될 수 있습니다!

결정 트리(Decision tree) & 랜덤 포레스트(Random forest)

이 모델들은 지난 게시 글에서 확인 할 수 있습니다. 여기를 눌러 확인해보세요.

비지도학습 모델

지금부터는 비지도 학습 모델을 다룰 것입니다. 다시 말하지만 비지도 학습 모델의 데이터는 라벨링이 되어있지 않기 때문에 어떤 결과가 나올지는 알 수 없습니다.

K 평균 군집화

K 평균 군집화 모델을 사용하려면, 우선 가진 데이터에 K개의 군집이 있다고 가정을 해야 합니신다. 실제로 데이터에 몇 개의 그룹이 존재하는지 모르기 때문에 여러 개의 K 값을 사용해 보고 시각화와 통계를 통해 어떤 K 값이 적절한지 확인해야 합니다.

K 평균 군집화 모델은 우선 K개의 군집을 형성하기 위해 최적의 K값을 정한 다음, 다음의 두 과정을 모든 포인트에서 반복합니다.

1.군집의 중심에 데이터 포인트를 할당

2.군집에 속해있는 모든 데이터 포인트의 평균으로 새로운 중심 생성

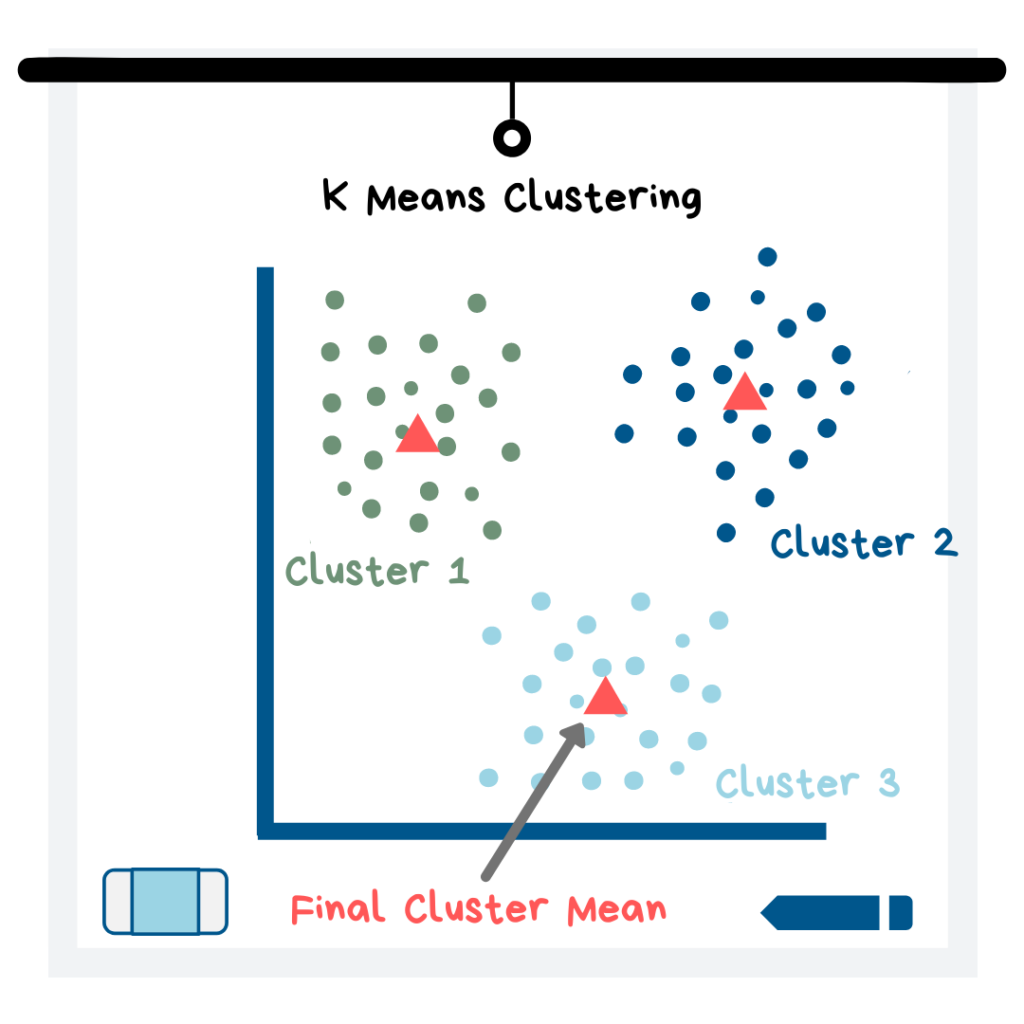
K 평균 균집화 개념도

밀집도 기반 클러스트링 (DBSCAN Clustering)

밀집도 기반 군집화 모델은 K-평균 군집화 모델과 달리 K 값을 입력하지 않고 모든 형태의 군집을 찾을 수 있습니다 (아래 그림 참조). 군집의 개수를 특정 하는 대신 군집 내부에 원하는 최소 데이터 점수와 데이터 포인트 주위의 반경을 정해줍니다. 그렇게 하면 밀집도 기반 군집화 모델은 군집을 찾아줄 것입니다! 그런 다음 적당한 데이터에 적합한 군집을 찾을 때 까지 변수들을 바꾸어주면 됩니다.

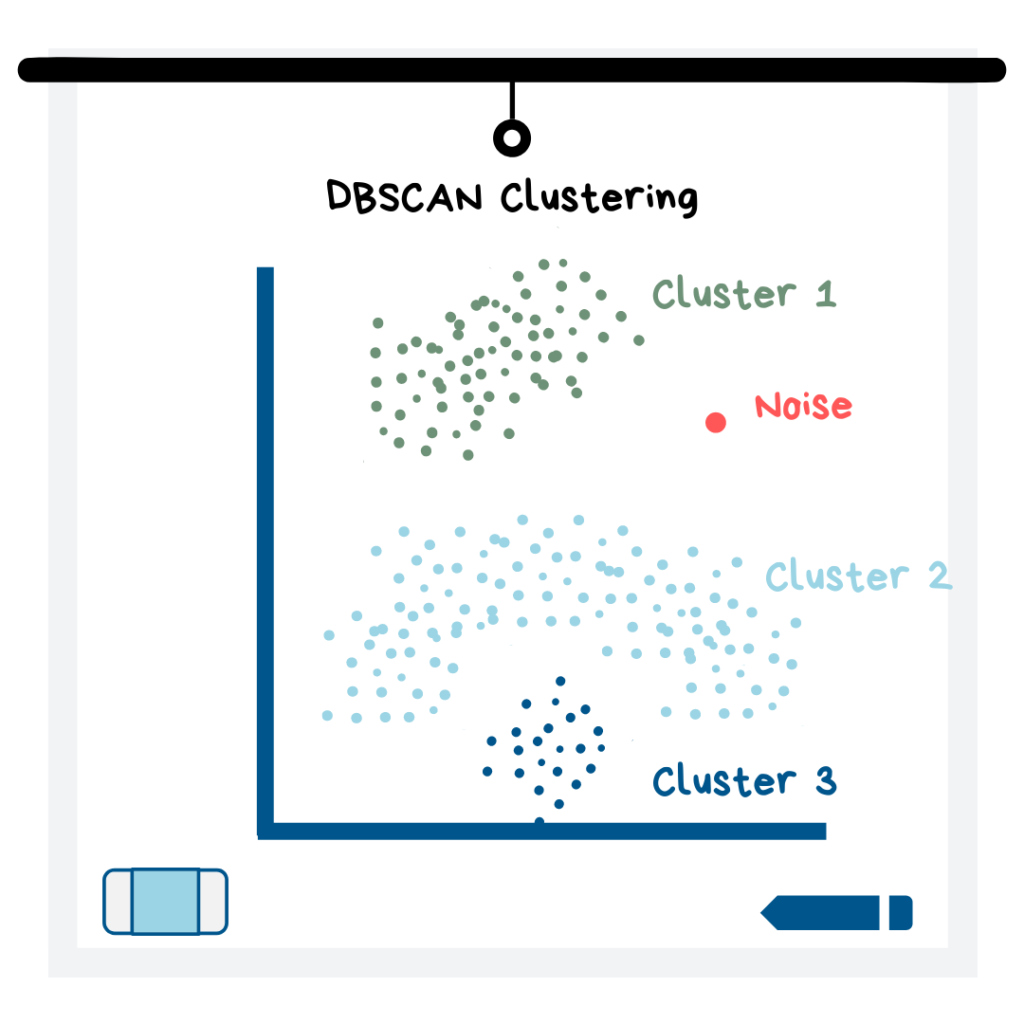
밀집도 기반 클러스트링 (DBSCAN Clustering) 개념도

또한 밀집도 기반 군집화 모델은 “잡음” 데이터 포인트를 찾아냅니다. (여기서 잡음은 모든 군집에서 떨어져있는 데이터입니다). 이 모델은 데이터 포인트들이 서로 가까이 있을 때 K-평균 군집화 모델보다 뛰어난 성능을 보입니다.

신경망 (Neural networks)

제 생각에 신경망은 가장 멋있고 신기한 모델입니다. 이 모델은 인간 뇌신경의 작동 방법을 모델로 하여 신경망이라고 부릅니다. 이 모델은 데이터 세트에서 패턴을 찾습니다. 종종 인간이 찾을 수 없는 패턴을 발견하기도 합니다.

신경망은 사진이나 소리와 같이 복잡한 데이터를 처리할 때 좋은 성능을 보입니다. 안면 인식부터 문서 분류까지 최근 개발된 소프트웨어에도 신경망 기술이 사용되었습니다. 또한 신경망은 지도 학습 모델과 자율 학습 모델 모두에 사용될 수 있습니다.

신경망은 작동의 기본 원리조차 이번 글에서 다루기에는 너무 복잡합니다. 만약 당신이 더 공부하고 싶다면 여기 ‘초심자’를 위한 가이드가 있습니다.

이 글이 모델들에 대한 여러분의 이해를 증가시켰을 뿐 아니라 얼마나 멋지고 유용한지 여러분들이 알게 해주었으면 좋겠습니다. 컴퓨터로 작업 / 학습을 시키면 우리는 가만히 앉아서 어떤 패턴을 발견하는지 지켜보기만 하면 됩니다. 때로는 전문가들조차 왜 그런 결론을 내렸는지에 대한 논리를 이해하지 못하기 때문에 혼란스러울 수 있지만, 우리는 컴퓨터가 예측을 잘 한다는 것에만 집중하면 될 것입니다.

인쇄하기